Có thể nói rằng toán học là một trong những lĩnh vực thuật ngữ và ký hiệu có hệ thống nhất trên thế giới. Vì vậy, không dễ để hiểu và nhớ tất cả các ký hiệu và thuật ngữ. Để có thể ghi nhớ lâu dài các ký hiệu toán học, chúng ta cần hiểu rõ các khái niệm của chúng chứ không phải là thực hành, thực hành và sử dụng chúng. Bài viết hôm nay sẽ giúp bạn tìm hiểu và ôn tập một trong những nguyên tắc cơ bản của toán học – đó là ký hiệu r. Vậy t r một bộ số đ ế là gì? Nó quan trọng như thế nào? Mời các bạn tiếp tục chú ý đến bài viết!
Trong toán học, tập hợp các số là gì?
Tìm hiểu về tập hợp số R
Bạn đang xem: Số r trong toán học là gì
Định nghĩa của tập số r:
Trong toán học, chữ r là viết tắt của tập hợp các số thực. Vậy câu trả lời cho câu hỏi “Bộ số là gì?” Có: r là tập hợp các số thực trong toán học.
Tập hợp các số thực r cũng là tập hợp các số lớn nhất. Nghĩa là, tất cả các tập hợp số khác là tập hợp con của tập r các số thực.
Tham khảo các công thức toán học khác:
- Giá trị tuyệt đối là gì? Cách tính giá trị tuyệt đối của một số thực
- Trung vị là gì? Định nghĩa, công thức và thuộc tính tiêu chuẩn
Một số bộ số khác trong toán học:
Trong toán học, có nhiều ký hiệu khác cho các bộ số. Có thể nói các mảng còn lại đều là các tập con của tập các số thực r. Vì vậy để có thể trả lời câu hỏi “Tập hợp con số là gì?” Một cách chính xác và dễ dàng hơn, chúng ta cần biết một chút về các tập hợp con của nó.
n – là tập hợp các số tự nhiên:
Ví dụ:
Tập hợp n gồm các số 0, 1, 2, 3, 4, 5, 6, 7, …
Biểu diễn của tập hợp các số tự nhiên n như sau:
n = 0, 1, 1, 3, 4, 5, 6, …
Trục biểu diễn dãy số tự nhiênn * – là tập hợp các số tự nhiên khác 0:
Nó chỉ cách tập số tự nhiên n một điểm và tập số n * không có số 0.
Ví dụ:
Bộ n * gồm các số: 1, 2, 3, 4, 5, 6, 7, 8, …
Các ký hiệu cho tập hợp các số tự nhiên khác 0 n * như sau:
n * = 1, 2, 3, 4, 5, 6, 7, …
z – là một tập hợp các số nguyên
Tập hợp các số nguyên là tập hợp các sách tự nhiên thuộc tập hợp n và tương hỗ của nó, tức là các số nguyên âm (-1, -2, -3, -4, -5, -6, …) và chẵn số 0.
Ví dụ:
Tập hợp z các số nguyên bao gồm các số sau: …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …
Kí hiệu cho tập hợp z các số nguyên như sau:
z = …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …
q – là tập hợp các số hữu tỉ:
Số hữu tỉ là số thập phân xuất hiện dưới dạng phân số. Đó là, nó được viết là ab. Đặc biệt, đây phải là số thỏa mãn điều kiện a, b thuộc tập z các số nguyên và b ≠ 0 được coi là số hữu tỉ. Ngoài ra, số hữu tỉ cũng được biểu diễn dưới dạng số thập phân vô hạn “không tuần hoàn”.
Ví dụ:
Tập hợp số hữu tỉ q gồm các số sau: 54, 13, 18, 35, 94,…
Biểu diễn của tập số hữu tỉ q như sau:
q = 54, 13, 18, 35, 94,…
i là tập hợp các số vô tỉ:
Điều ngược lại hoàn toàn với số hữu tỉ. Số vô tỉ là số thập phân vô hạn “tuần hoàn”. Có thể nói i là tập hợp các số không vô tỉ.
Ví dụ: Tập hợp các số vô tỉ bao gồm: π, e, 2, -5 …
Chúng ta có ký hiệu sau cho tập hợp các số vô tỉ:
i =, e, 2, -5…
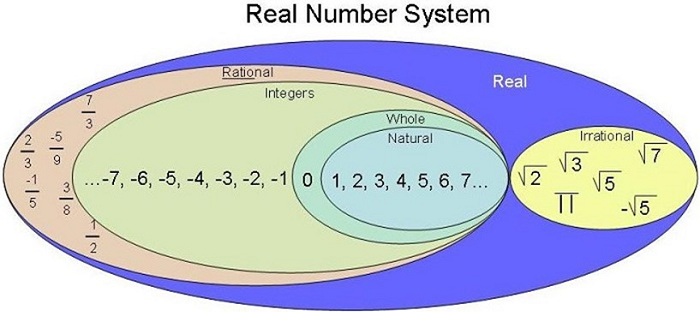
Hệ thống số thực r
Số thực là gì?
Sau khi hiểu định nghĩa, hãy cho biết khái niệm về số của r là gì? Chúng ta biết rằng r là ký hiệu cho tập hợp các số thực. Vậy số thực là gì? Số thực là gì?
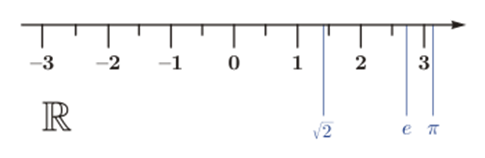Biểu diễn tập hợp số thực R trên trục sốCác số thực được coi là tập hợp “mẹ” của các tập hợp số trên. Các tập hợp số tự nhiên, số nguyên, số hữu tỉ và số vô tỉ (kể cả số 0) đều là tập con của tập mẹ, tập r các số thực.
Mặc dù vậy, tập hợp số thực vẫn không phải là tập hợp số lớn nhất. Tập hợp số phức c mới là tập hợp số lớn nhất.
Theo định nghĩa và tập hợp của tập số thực r, có thể nói rằng tính chất của tập số thực r là một tập vô hạn và không đếm được. Tập hợp các số thực lớn hơn nhiều lần so với tập hợp của tất cả các tập hợp khác (bộ số n, n *, z, q, i)
Tính từ “real” trong số thực này xuất hiện lần đầu tiên vào thế kỷ XVI. Nhờ công của một nhà khoa học nổi tiếng, cơ sở cho nhiều phân tích trong lĩnh vực toán học. Anh ấy là Descartes thực sự.
Đối với anh ấy, số thực là các giá trị liên tục được biểu diễn dọc theo một đường thẳng.
Các thuộc tính của tập hợp r các số thực:
- Mọi số thực (trừ số 0) đều là số dương và số nghịch đảo của nó (số âm). Ví dụ, nếu chúng ta có một số dương 1, ngược lại của nó là -1 (một số âm).
- Tổng (kết quả của phép cộng) hoặc tích (kết quả của phép nhân) của hai số thực. Một số không âm luôn là một số thực không âm.
- Đây được coi là tính chất cơ bản và dễ nhận biết nhất của tập hợp các số thực. Số thực được coi là một tập hợp vô hạn các số có vô hạn và không đếm được.
- Phép đo các đại lượng liên tục có thể được biểu diễn bằng số thực.
- Các số thực có thể biểu diễn được biểu diễn ở dạng số dưới dạng số thập phân (phân số).
Sau khi trả lời câu hỏi “Tập hợp r là gì? ” và hiểu các tính chất của tập hợp r các số thực. Tiếp theo, chúng ta cùng áp dụng và xem lại tập hợp các số thực r.
Một số dạng của tập hợp các số thực r:
Ngoài Câu hỏi thường gặp về xác định tập hợp các số thực, chẳng hạn như r có phải là tập hợp số không? Z biểu diễn tập hợp số nào? Sự khác nhau giữa số hữu tỉ và số vô tỉ là gì? ,… và các câu hỏi về các ký hiệu liên quan, liên quan đến các bài tập về các tập hợp số như ∈, ∪, ∩, /,.. Dưới đây là bảng giải thích và định nghĩa của các dấu hiệu và ký hiệu đó:
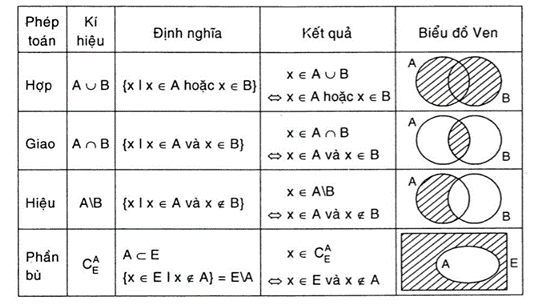Một số kí hiệu gắn liền với bài tập về tập hợp sốLoại 1: Câu hỏi về thực hành số:
Cách sử dụng;
Các ký hiệu cài đặt số như trên.
Chúng ta có mối quan hệ sau giữa các bộ số: n ⊂ z ⊂ q ⊂ r; i.
với:
n là tập hợp các số tự nhiên
z là tập hợp các số nguyên
q là tập hợp các số hữu tỉ
z là tập hợp các số vô tỉ
r là tập hợp các số thực
Dạng 2 là tìm ẩn số trong phương trình:
Cách sử dụng:
- Sử dụng các thuộc tính của các phép toán để tính toán.
- Sử dụng mối quan hệ giữa các số hạng trong tổng tính toán và hiệu số. Điều tương tự cũng áp dụng cho các phép toán nhân và chia.
- Sử dụng các quy tắc ngắt dấu ngoặc đơn và chuyển vị.
Bảng 3: Đánh giá một biểu thức
Cách sử dụng:
- Phối hợp nhân, chia, cộng, trừ và lũy thừa.
- Luôn nhớ giảm điểm số
Tóm tắt:
Tổng hợp những khái niệm trên đây về tập số thực r được Legoland tổng hợp từ sách giáo khoa, hi vọng sẽ giúp các em học sinh hiểu được tập hợp số là gì và các công thức liên quan đến tập số thực. Được rồi.
Xuất bản ngày 14 tháng 10 năm 2021 7:45 sáng
